Print version:  Close window    Print

International Conference on Magnetic Resonance Microscopy

Magnetic Resonance in Porous Media I - L-020

The Generalized Phillips-Twomey Method for NMR Relaxation Time Inverse

Y. Gao1, 2*, L. Xiao1, Y. Zhang2, Q. Xie3
  • 1. State Key Laboratory of Petroleum Resource and Prospecting, China University of Petroleum, Beijing, China
  • 2. College of Science, China University of Petroleum, Beijing, China
  • 3. Key Laboratory of Shale Gas Exploration, Ministry of Land and Resources, Chongqing Institute of Geology and Mineral, Chongqing, China

It is a crucial step to invert the nuclear magnetic resonance (NMR) relaxation time for NMR data processing and interpretation. And the inversion is Fredholm integral equation of the first kind. Due to its ill-posedness, numerical solutions to this type of equations are often found much less accurate and bear little resemblance to the true solution. In this paper, we prove the existence, uniqueness, stability and convergence of the generalized Phillips-Twomey regularization method for solving this type of equations in the following way.
Suppose we try to solve the operator equation Kf=g. Considering the existence of the solution, we call fq a quasi-solution if it satisfies ||Kfq-g||=inf{||Kf-g||:f ∈ W22(a,b)}. Since, the quasi-solutions are not unique, let FK be the set of all the quasi-solutions. And we call the least W22 norm one in FK the generalized Phillips-Twomey solution. Note that the W22 norm of a function f in the Soblev space is ||f||W2=||f||2+||f'||2+||f''||2. Thereby, the generalized Phillips-Twomey solution exists and is unique but is not stable.
Taking the inevitable errors into account, we can only obtain an approximation ge to g with ||ge-g||≤δ, where δ is a constant. Let fs be the generalized Phillips-Twomey solution, ε =inf{||Kf-ge||:f∈W22(a,b)} and Qδ={f∈W22(a,b):||Kf-ge||≤ε+2δ}. We obtain the following optimization problem:
inf{||f||W:f∈Qδ} (1)
The solution of Problem (1) is well-posed and near the real solution. However, it is basically impractical to solve Problem (1) due to the difficulties in determining the set Qδ during the computation. Fortunately, we can prove that the minimizer fδ of Problem (1) satisfies fδ=0 or ||Kfδ -ge||=ε+2δ. Hence, Problem (1) can be reformulated into the following:
inf ||f||W s.t. ||Kf-ge||= ε+2δ
By applying the Lagrangian multiplier method, we obtain:min{||Kf-ge||2+ α||f||W2:f∈ W22(a,b)} and solve it accordingly.
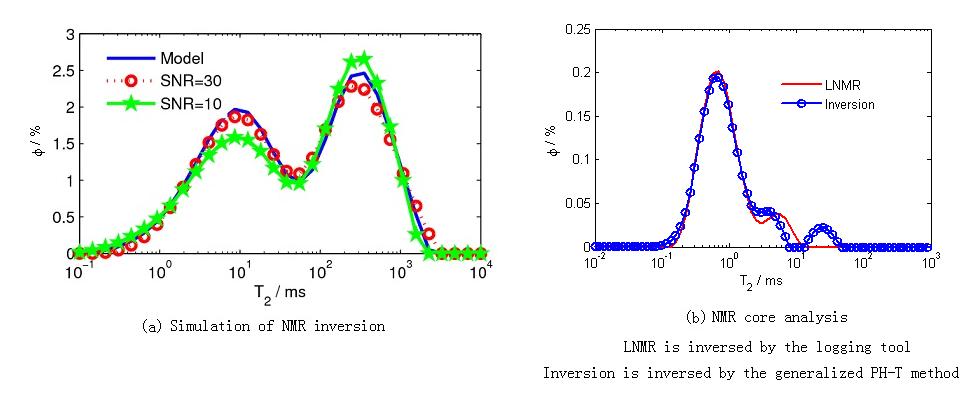
In this paper, a numerical simulation and a core analysis arising from NMR transverse relaxation time inversion are conducted to show the effectiveness of the generalized Phillips-Twomey method. Both show that the inversions are suit to the model and reality respectively. The statistics of the solutions to the NMR simulation are shown in Table 1.

  Error in the effective porosity Error in water saturation Mean of the residual Std of the residual Maximum of the residual
SNR=30 -0.6177 -1.5149% -0.0193 0.0935 0.2219
SNR=10 -1.1935 -3.7537% -0.0373 0.1595 0.3824
Table 1 Comparison of effective porosities, water saturations and residuals
Figure 1 shows the inversions.
Get
Figure 1 Inversions


Keywords. Generalized Phillips-Twomey method,Ill-posedness,NMR Relaxation Time Inverse,Numerical simulation,Core analysis


  • [01]  Wang J. Y., (1998), Inverse Theory in Geophysics, China University of Geosciences Press
  • [02]  Yang W. C. , (1996), Inverse Theory and Methods in Geophysics, Geosciences Press
  • [03]  BI B., WANG D. M, (2008), Multi-constraint smooth method for solving fredholm integral equation of first kind, JOURNAL OF HARBIN INSTITUTE OF TECHNOLOGY, 40(3):440-442
  • [04]  Dunn K J, Latorraca G A, Warner J L, (1994), On the calculation and interpretation of NMR relaxation time distribution, SPE, SPE 28367, 69th Annual SPE Technical Conference and Exhibition, New Orleans, 45-54
  • [05]  XIAO L Z, Zhang H. R, LIAO G Z, et al. , (2012), Inversion of NMR relaxation in porous media based on Backus-Gilbert theory, Chinese J. Geophys. , 55(11):3821-3828
  • [06]  Phillips D.L. , (1962), A Technique for the Numerical Solution of Certain Integral Equations of the First Kind, J. ACM, 9: 84-87
  • [07]  Twomey S. , (1963), On the Numerical Solution of Fredholm Integral Equations of the First Kind by the Inversion of Linear Systems Profuctuced by Quadrature, J. ACM, 10: 97-101
  • [08]  Zhang Y. H. , (1989), Regulazation Method for Fredholm Integral Equations of the First Kind , Journal of Hebei Normal University (Natureal Science Edition), 13(4) : 45-53
  • [09]  Zhang G. Q., Lin Y. Q. , (1987), Functional Analysis, Peking University Press
  • [10]  Walter Rudin, (2004), Functional Analysis(Second Edition), Beijing: China Machine Press
Print version:  Close window    Print